Additional information about Beam Design¶
Important
All our Watch and Learn section for SOFiSTiK Analysis + Design is under revision. It will be upgraded step by step.
The Beam Dialog analyzes and designs the selected beam members in the Ultimate and Serviceability Limit State according to the EN 1992-1-1:2004.
Please refer to the Supported Calculation and Design Codes page for an overview of the supported design codes.
If an other design code is used, then the program will use the design code EN 1992-1-1:2004 as a fallback design code.
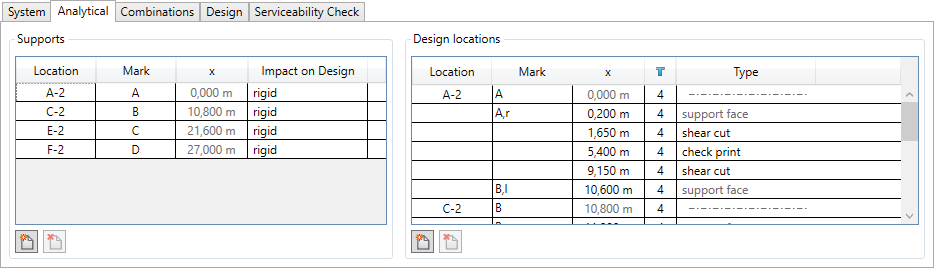
The Analytical Tab is able to modify the support conditions between rigid, indirect and hinged support situations. The program will interpret these as Masonry or Concrete (direct or indirect) support situation. This will affect the printout, what kind of rules are allowed according to the design code.
In the following Figure, the column x and Type are editable and will be interpreted and appear in the resulting printout.
For example: If a shear cut is defined at x=0.75 m, then the shear force will be reduced to the support axis. If no support situation was detected, then there is the possibility to define a new support situation.
The Design Tab allows to control the analysis and design with following features:
Control uniaxial and biaxial bending design
Select net or gross sectional area design
Support moment reduction and smoothing
Moment redistribution
Shear design with given strut angle
The reduction of the shear force depends on the analytical support situation.
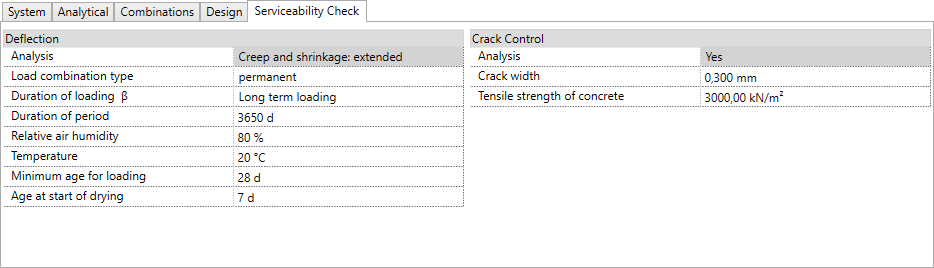
The Serviceability Check Tab allows to check following features:
Minimum reinforcement areas
Control of cracking without direct calculation
Calculation of crack widths
Calculation of creep and shrinkage
Checking deflections by calculation
The program will automatically take and distribute the decisive reinforcement of each layer along the beam members. The crack control is using the reinforcement bar diameters defined in the cross section dialog.
Checking the deflections by calculation is implemented according to the EN 1992-1-1, Ch. 7.4.3. It is calculating the linear and nonlinear curvatures in uncracked and fully cracked state. The equation EN 1992-1-1, 7.4.3 (7.18) interpolates the curvatures in both states and then calculates the deflections by numerical integration.
The standard code EN 1992-1-1 recommends to use the permanent load combination for the deflection by calculation. In some cases if requested the frequent or rare load combination can be used as well.
The effects of creep and shrinkage will be considered in each span beam member. The span with the maximum deflection will have the maximum creep and shrinkage curvatures and all the other spans will be scaled with a factor from 0.0 to 1.0 depending on their deflections.


