Superposition according to Russian SP 20.13330.2016: Loads and Actions#
Introduction#
This document provides a short introduction in the use of the program MAXIMA for combinations according to the Russian code SP 20.13330.2016: Loads and Actions
Hint
This tutorial is based on SP 20.13330.2016 and SP 63.13330.2012
Theoretical Background#
In the code SP 20.13330.2016: Loads and Actions a main combination is given in formula (6.1):
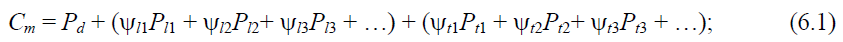
- where: Pd - permanent actions
Pl - long-term variable actions Pt - short-term variable actions
Here two two formulas are described:
for the design of the group 1 (ultimate load) using safety factors γf
Cm = γf ∙ Pd + (γf ∙ ψl1 ∙ Pl1 + γf ∙ ψl2 ∙ Pl2 + γf ∙ ψl3 ∙ Pl3 + …) + (γf ∙ ψt1 ∙ Pt1 + γf ∙ ψt2 ∙ Pt2 + γf ∙ ψt3 ∙ Pt3 + …)
for the design of the group 2 (serviceability) without safety factors γf
Cm = Pd + (ψl1 ∙ Pl1 + ψl2 ∙ Pl2 + ψl3 ∙ Pl3 + …) + (ψt1 ∙ Pt1 + ψt2 ∙ Pt2 + ψt3 ∙ Pt3 + …)
for special combinations the first equation should be used with finally superposition inclusive the special load Ps (e.g. accidental combinations with accidental action)
Cs = Cm + Ps
Regradless of the use of the safety factors, the equation 6.1 has two parts of variable actions:
first part for long-term variable actions
(ψl1 ∙ Pl1 + ψl2 ∙ Pl2 + ψl3 ∙ Pl3 + …) with ψl1 = 1.0 and ψl2 = ψl3 = 0.95
It means: Pl1 is the leading long-term action and Pl2 and Pl3 are accompanying long-term actions.
second part for short-term variable actions
(ψt1 ∙ Pt1 + ψt2 ∙ Pt2 + ψt3 ∙ Pt3 + …)
for the design of the group 1 (ultimate load) with ψt1 = 1.0 , ψt2 = 0.9 and ψt3 = ψl4 = 0.7
for special combinations with ψt1 = 0.5 , ψt2 = ψt3 … = 0.3
It means: Pt1 is the first leading short-term action, Pt2 is the second leading short-term action and Pt3 and Pt4 are accompanying short-term actions
Note
The coefficients ψt for the design of the group 1 (ultimate load) are preset at the actions. The modified coefficients for special combinations are to be taken into account in the combination definition in MAXIMA.
Objectives#
Generate the system inclusive the design code, materials, cross sections
Generate the actions with the task Action Manager or with the program SOFiLOAD
Generate loads inside SOFiPLUS or with the program SOFiLOAD
Run linear analysis
Generate action combinations
Generate superpositions
Project Description#
In the given file a 2D plate system is generated. The example is only made for demonstration of the default actions with the program SOFiLOAD and of the definition of the combinations with the program MAXIMA. The selected design code ist SP 63-13330 Concrete and Reinforced Concrete Structures (2012).
Geometry#
A simple 2D plate, which is devided in three part (three groups of plane elements), is presented. The direction of grafity is the Z direction.

Materials#
Number |
Grade |
Notes |
|---|---|---|
1 |
B 35 (SP 63.13330) |
concrete fc = 19.5 MPa |
2 |
A 500 (SP 63.13330) |
reinforcing steel fy = 435 MPa, ft = 600 MPa |
Actions and Load Cases#
Action and its Category |
Title |
Load Cases |
|---|---|---|
G_C |
dead load concrete, category C, permanent |
1 |
G_S |
dead load soil, category S, permanent |
|
Q |
uniform distributed loads, variable short-term |
11,12 conditional |
S |
snow loading, variable short-term |
21,22,23 conditional |
W |
wind loading, variable short-term |
31,32,33 exclusive |
LI |
fixed installations, variable long-term |
41,42 |
LC |
loaders and electric cars, variable long-term |
51,52 conditional |
LM |
stored materials and products, variable long-term |
61,62,63 |
The actions and the loads are defined with the program SOFiLOAD. Here only default actions are used. Therefore, only the action names have be input. The corresponding safety factors and combination coefficients are added automatically.
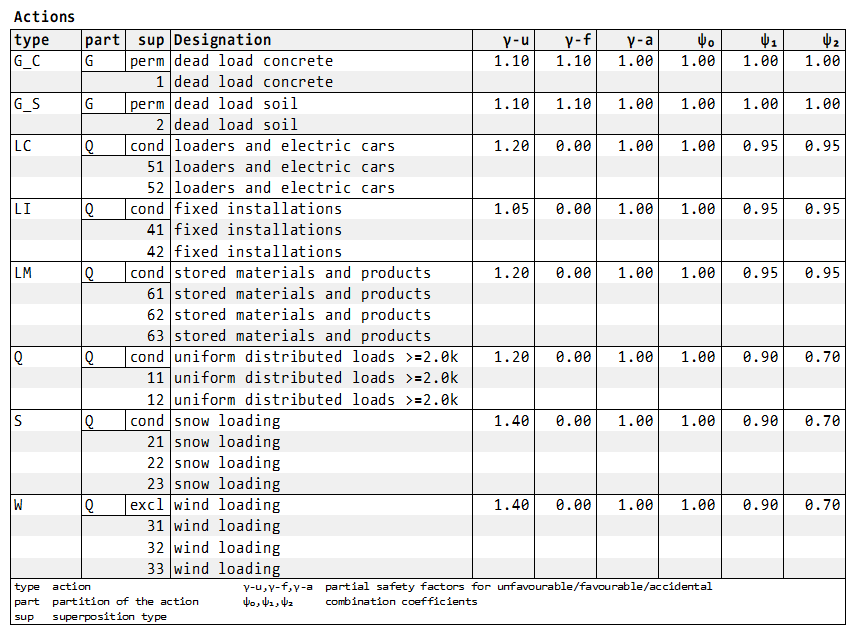
- The combination coefficients are defined here as follows:
factors ψl1 and ψt1 are defined at ψ0
factors ψl2 (= ψl3) and ψt2 are defined at ψ1
factor ψt3 is defined at ψ2
The printout of the table Actions inclusive the corresponding load cases is as follows:
Action Combinations using Program MAXIMA#
For the combination equation (6.1) according to SP 20.13330.2016 it is necessary to make three pre-superpositions and finally an envelope about their results. The procedure is necessary, as in each case for the short-term loads and long-term loads the leading and the accompanying actions have to be determined.
For demonstration purpose the superposition value is here the nodal value PZ (support reaction). The node 12 is selected for the prinout.
1st pre-superposition for the permanent actions
An explicit defined combination is created using the safety factors for the permanent actions. The type of the results is none, because the resulting load cases should not be considered for a later design. The generated load case numbers are 2155 and 2156.
The MAXIMA input is:
+PROG MAXIMA
HEAD pre-superposition permanent actions
echo load,fact
comb 1 extr expl type none base 2100
! ADD {G} facu gamu facf gamf ! all permanent actions
!or
ADD G_C facu gamu facf gamf ! action G_C
ADD G_S facu gamu facf gamf ! action G_S
supp 1 extr mami etyp node type pz from 12 ! from 12 only for full printout with echo
END
2nd pre-superposition for the long-term actions
An explicit defined combination is created using the safety factors and combination coefficients for the long-term actions. The type of the results is none, because the resulting load cases should not be considered for a later design. The generated load case numbers are 2255 and 2256.
With the input line ADD {Q1} facu psiu facf 0, it is defined that the leading action should be determined with the unfavourable factor γf ∙ ψ0 = literal psiu . The definition of the record ADA LI,LC,LM determines that only the long-term actions should be used. The accompanying long-term actions get the unfavourable factor γf ∙ ψ1 = literal ps1u.
+PROG MAXIMA
HEAD pre-superposition long-term actions
echo load,fact
comb 2 extr expl type none base 2200
ADD {Q1} facu psiu facf 0 ! first leading action
ADA LI,LC,LM ! use only long-term actions LI,LC,LM
ADD {QI} facu ps1u facf 0 ! accompanying actions
ADA LI,LC,LM ! use only long-term actions LI,LC,LM
supp 2 extr mami etyp node type pz from 12 ! from 12 only for full printout with echo
END
3rd pre-superposition for the short-term actions
An explicit defined combination is created using the safety factors and combination coefficients for the short-term actions. The type of the results is none, because the resulting load cases should not be considered for a later design. The generated load case numbers are 2355 and 2356.
With the input line ADD {Q1} facu psiu facf 0, it is defined that the 1st leading action should be determined with the unfavourable factor γf ∙ ψ0 = literal psiu . The definition of the record ADA Q,S,W determines that only the short-term actions should be used. The determination of the 2nd leading action is defined by the input line ADD {Q2} facu ps1u facf 0, where the unfavourable factor is γf ∙ ψ1 = literal ps1u. The accompanying short-term actions get the unfavourable factor γf ∙ ψ2 = literal ps2u.
For the design of the group 1 (ultimate load DESI):
+PROG MAXIMA
HEAD pre-superposition short-term actions
echo load,fact
comb 3 extr expl type none base 2300
ADD {Q1} facu psiu facf 0 ! first leading action
ADA Q,S,W ! use only short-term actions Q,S,W
ADD {Q2} facu ps1u facf 0 ! second leading action
ADA Q,S,W ! use only short-term actions Q,S,W
ADD {QI} facu ps2u facf 0 ! accompanying actions
ADA Q,S,W ! use only short-term actions Q,S,W
supp 3 extr mami etyp node type pz from 12 ! from 12 only for full printout with echo
END
For the design of the group 1 (accidental load ACCI): Here the modified combination coefficients ψt1, ψt2, ψt3 are considered in the formulas for the unfavourable factor FACU.
+PROG MAXIMA
HEAD pre-superposition short-term actions
echo load,fact
comb 3 extr expl type none base 2300
ADD {Q1} facu '=0.5*gamu' facf 0 ! first leading action
ADA Q,S,W ! use only short-term actions Q,S,W
ADD {Q2} facu '=0.3*gamu' facf 0 ! second leading action
ADA Q,S,W ! use only short-term actions Q,S,W
ADD {QI} facu '=0.3*gamu' facf 0 ! accompanying actions
ADA Q,S,W ! use only short-term actions Q,S,W
supp 3 extr mami etyp node type pz from 12 ! from 12 only for full printout with echo
END
final envelope
At last the final envelope of the resulting load cases from the pre-superpositions should be done. For this a standard combination is defined with the specification of the resulting load cases from the pre-superpositions. The type of the resulting load cases 2455 and 2456 is desi in order for using them in a later design.
The MAXIMA input is as follow for the design of the group 1 (ultimate load DESI):
+PROG MAXIMA
HEAD envelope
echo load,fact
comb 4 extr stan type desi base 2400 ! type desi for a later design
LC 2155,2156 type AG1 ! load cases from pre-superposition permanent actions in permanent load group AG1
LC 2255,2256 type A2 ! load cases from pre-superposition long-term actions in alternative load group A2
LC 2355,2356 type A3 ! load cases from pre-superposition short-term actions in alternative load group A3
supp 4 extr mami etyp node type pz from 12 ! from 12 only for full printout with echo
END
The final MAXIMA input reads for the special combination of the group 1 (accidental load ACCI):
+PROG MAXIMA
HEAD envelope + accidental action
echo load,fact
comb 4 extr stan type acci base 2400 ! type desi for a later design
LC 71,72 type A10 ! load cases action A exclusive in alternative group A10
LC 2155,2156 type AG1 ! load cases from pre-superposition permanent actions in permanent load group AG1
LC 2255,2256 type A2 ! load cases from pre-superposition long-term actions in alternative load group A2
LC 2355,2356 type A3 ! load cases from pre-superposition short-term actions in alternative load group A3
supp 4 extr mami etyp node type pz from 12 ! from 12 only for full printout with echo
END
Remarks#
For the workflow of the superposition with equation (6.1) according to SP 20.13330.2016 it is recommend to use the input with Teddy of the program MAXIMA. The definition of the combinations with the SSD task Define Combinations is not possible, because in this the used actions cannot be selected for an explicit defined combination with actions groups (2nd and 3rd pre-superpositin record ADA).
The superposition for the serviceability limit state is analogous, however without the safety factors γf.